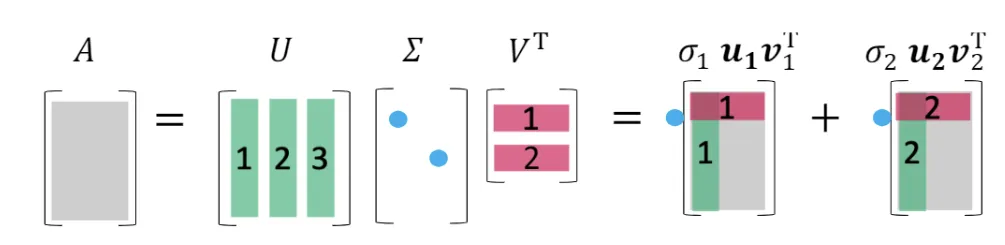奇异值分解(SVD)#
奇异值分解(singular value decomposition, SVD),说的是任意矩阵 A∈Cm×n ,都可以分解成以下形式
A=u1σ1v1∗+u2σ2v2∗+⋯+urσrvr∗=(u1…u2um)(diag(σ1,σ2,…,σr)000)v1∗v2∗⋮vn∗=UΣV∗
其中 r 是矩阵 A 的秩, u1,u2,…,um 为 AA∗ 的特征向量, v1,v2,…vn 为 A∗A 的特征向量
U 和 V 满足
U∗UV∗V=I=I即 U 和 V 均为酉矩阵。
且 σ1≥σ2≥⋯≥σr>σr+1=σr+2=⋯=σn=0 。
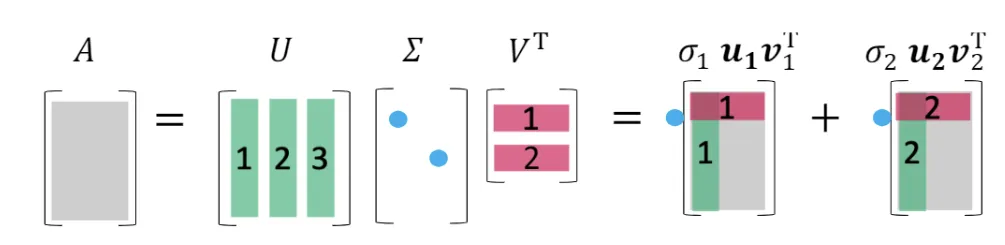
奇异值分解表明了任意矩阵都可以拆分成r个秩为1的矩阵之和。酉矩阵表明 u1 和 v1 的长度均为 1。则 σi 的大小描述了拆分成的这个矩阵的重要程度, σi 越大,说明 uiσivi∗ 这一项越重要。这就揭示了奇异值分解在数据降维、图像压缩、统计分析(如:主成分分析)方面大有用处。
相比于特征值分解,奇异值分解的优势多多。
-
对矩阵的要求少
特征值分解要求 A 为方阵,且可对角化。而奇异值分解对 A 没有什么限制。
-
稳定性
当 A 中一个值微小的改变时,特征值分解的 Λ 可能会发生比较大的改变。但是奇异值分解的 Σ 只会发生很小的改变。并且这些改变都发生在靠后的、 σi 更小的项里。
截取k项#
由于 σi 的大小是从大到小排列,因此我们可以只取前面 k 项,得到
u1σ1v1∗+u2σ2v2∗+⋯+ukσkvk∗=UkΣkVk∗其中 Uk 为 m×k 矩阵,Σk 为 k×k 对角阵, V 为 n×k 矩阵。
当 k=r 时,则
A=UkΣkVk∗仍然成立,此时相当于对A进行了无损压缩。
当 k<r 时,σ1 最小的 r−k 项被舍弃了,但是得到的新矩阵和原来的矩阵仍然是相近的,相当于一个有损压缩。
A≈UkΣkVk∗显然,新矩阵的秩为k,此时相当于做了一个数据降维。
存在性证明#
引理1:对称矩阵均为半正定矩阵(半正定矩阵:特征值均非负的矩阵)
先证明λ为实数
S∗Sx⇒x∗Sx∗(Sx)(x∗S)x(λ−λ)∣x∣2=S=λx=λx∗=λx∗x=λ∣x∣2=λx∗x=λ∣x∣2=0
又因为特征向量 x 非零,得 λ=λ,即 λ 为实数
再证明 λ 非负
x∗A∗Ax∣Ax∣2∣λ∣2=(λx∗)(λx)=∣λ∣2∣x2∣=∣x∣2∣Ax∣2≥0
引理2:rank(A∗A)=rank(AA∗)=r
由 Ax=0⇒A∗Ax=0 得
N(A∗A)⊂N(A)
若 A∗Ax=0,则
x∗A∗AX=(Ax)∗Ax=∣Ax∣2=0
Ax=0
所以
N(A)⊂N(A∗A)
有
N(A)dimN(A)n−rank(A)rank(A)=N(A∗A)=dimN(A∗A)=n−rank(A∗A)=rank(A∗A)
同理可证明rank(A∗)=rank(AA∗),故原式成立
引理3:A∗A 和 AA∗ 均有 r 个相同的正特征值。
首先证明均有 r 个特征值:
由于 A∗A 为对称矩阵,由于对称矩阵一定是正规矩阵,由谱定理有
A∗A=UΛU∗
由引理1,特征值不可能为负。且 Λ 中非零元素个数其实就是 rank(Λ)
则正特征值个数 rank(Λ)=rank(A∗A)
对 AA∗ 同理
再证明 A∗A 的正特征值也是 AA∗ 的正特征值:
A∗AxAA∗AxAA∗(Ax)=λx=λAx=λ(Ax)
由 λ=0 得 Ax=0,故 Ax 是 A∗A 的一个特征向量,对应的特征值为 λ。
反之可证 AA 的正特征值也是 A∗A 的特征值,则两矩阵拥有相同的一组正特征值。
由引理3,我们设这一组相同的特征值为 λi(i≤r) 并从大到小排列,λ1≥λ2≥⋯≥λr>λr+1=λr+2=⋯=λm=0。
证明是构造性的
对 A∗A 谱分解可以求出 V 和 λi,设 V 的第 i 列为 vi,对应特征值 λi。
设 V=(VrV0) ,前 r 列为 Vr,剩下 m−r 列为 V0。
U=(UrU0),前 r 列为 Ur,剩下 n−r 列为 U0。
当 i>r 时,由 A∗Avi=0 两边左乘以 vi∗,易得 Avi=0,故有 AV0=0。
等价变换原式
AAVA(VrV0)AVr=UΣV∗=UΣ=(UrU0)(Σr000)=UrΣr(1)(2)再令
σiΣr=λi=diag(σ1,σ2,…,σr)Vr、Σr 均已构造出来,则只需构造符合 (1) 的 Ur,且 ui(i≤r)满足以下条件:
- ui 为单位向量。
- ui⊥uj(i=j)。
- ui 是 AA∗ 的特征向量。
令 ui=σi1Avi,下面证明其满足三个条件
ui∗ui=σi21vi∗A∗Avi=λi1vi∗λivi=1ui∗uj=σiσj1vi∗A∗Avj=σiσj1vi∗vj由 vi 和 vj 正交知上式等于 0,即 ui 和 uj 也正交。
AA∗ui=σi1AA∗Avi=σiAvi=λiui证毕。
与四个基本子空间的关系#
- Vr=(v1,v2,…,vn)是A的行空间C(A∗)的一组标准正交基;
- V0=(vr,vr+1,…,vn)是A的零空间N(A)的一组标准正交基;
- Ur=(u1,u2,…,uu)是A的列空间C(A)的一组标准正交基;
- U0=(ur,ur+1,…,un)是A的左零空间N(A∗)的一组标准正交基。
线性代数中非常重要的子空间,和SVD就这样巧妙地联系在一起了,由 V∗V=I 和 U∗U=I,又能再次验证四个基本子空间的两组垂直关系:
C(A)⊥N(A∗)C(A∗)⊥N(A)为了结论的泛用性,上面的证明是在复数域 C 下进行的,当然换成实数域也是同理的,只要将 A∗ 换成 AT 即可。