投影矩阵的推导#
假设我们想把一个向量 b 投影到线性空间 S 中,应该怎么做呢。
设投影后的向量为 p,则有 p∈S,设误差向量(error vector)e=b−p,则 e 应与 S 正交。投影就是将向量分为两部分 b=p+e,一部分在 S 中,另一部分与 S 正交,然后取其中的 p。也可以用图像直观理解:
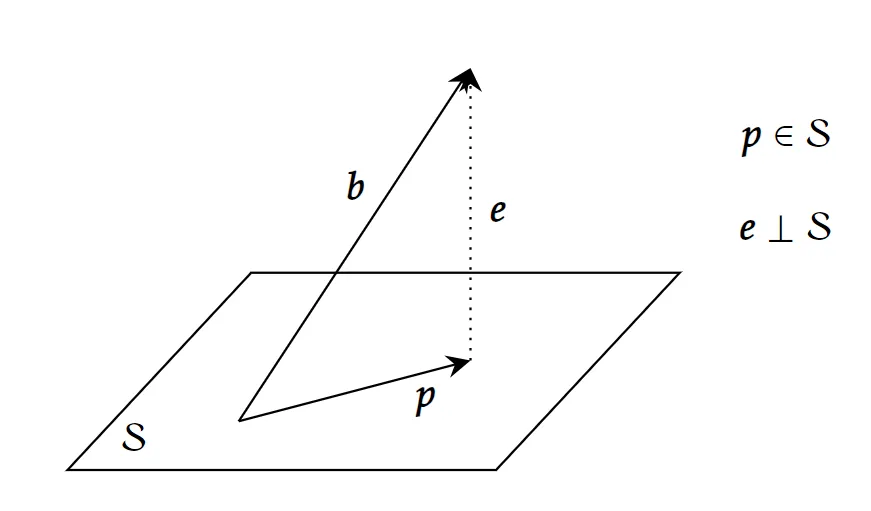
要求得 p,只需要将 p∈S(1) 和 e⊥S(2) 这两个条件翻译成线性代数的语言即可。
首先,我们要先表达线性空间 S,设 S⊂Pm,dimS=n,取 S 的一组基,作为矩阵 Am×n 的列向量,则 S 就是 A 的列空间,S=C(A)。
- 然后要翻译 p∈S,只需要令 p=Ax^,其中 x^为Pm 中的任意向量。
- 翻译 e⊥S,就是 e∈S⊥=C(A)⊥=N(AT),即 ATe=0。
得到方程组
{p=Ax^ATe=0ATeAT(b−Ax^)ATbx^p=0=0=ATAx^=(ATA)−1ATb=A(ATA)−1ATb令 P=A(ATA)−1AT,称 P 为 S 的投影矩阵(projection matrix),则要将 b 投影至 S ,只需左乘P即可,p=Pb。
这里的 (ATA)−1 不能拆作 A−1(A−1)T,因为 A 不一定为方阵,当 n<m 时,A 不可逆。当 n=m 时,A 必定可逆,因为列向量线性无关,然而当 n=m 时,投影的意义不大,易得 P=I ,投影不会改变任何东西。而 (ATA)−1 一定是可逆的(想想为什么?)。
当 A 是向量时#
当A是向量而非矩阵时,一切都没有变,我们仍然有 p=a(aTa)−1aTb,不过现在 aTa 是一个标量了,也可以写作
p=aTaaTba=a⋅aa⋅ba这和我们常见的向量投影到另一个向量的形式是一致的。
投影矩阵的特性#
1. 对称性#
PT=PPT=(A(ATA)−1AT)T=A((ATA)−1)TAT=A((ATA)T)−1AT=A(ATA)−1AT=P2. 幂等性#
Pk=P(k=1,2,…)直观理解,就是将 b 投影到 S 后,再投影一次,没有任何变化,因为 p 已经在 S 里了。
要证原命题,只需证 P2=P
P2=(A(ATA)−1AT)(A(ATA)−1AT)=A(ATA)−1(ATA)(ATA)−1AT=A(ATA)−1AT=P
两种极端情况#
1. 当 b∈S ,有 Pb=b#
已经在 S 上的向量再投影到 S 不会变化
因为 b∈C(A),则 ∃x,s.t.b=Ax,有:
Pb=A(ATA)−1ATAx=A(ATA)−1(ATA)x=Ax=b2. 当 b⊥S,有 Pb=0#
正交与 S 的向量,投影到 S 就只剩下一个点了
b⊥C(A)⇔b∈N(AT),故 ATb=0
Pb=A(ATA)−1ATb=A(ATA)−1(ATb)=0
投影的应用#
解一个无解的方程#
Ax=b 有时是无解的,因为 b 不在 A 的列空间 C(A) 中,于是我们可以将 b 投影到 C(A) 中。设 p 为 b 在 C(A) 的投影,则 Ax^=p 一定有解。
注意:这里的 p 不能和前文一样使用 A(ATA)−1ATb 求得,因为前面的 A 是列线性无关的,这里不一定。当 A 列线性无关时,x^ 有唯一解,当 A 列线性相关时,x^ 有无穷多解,无论如何,x^ 总是存在的。
回归正题,我们解出来的这个 x^ 虽然不是一个精确的解,但却是一个最好的解,这个 x^ 可以令 ∣∣Ax−b∣∣2 最小,这一点可以从两个角度证明:
- 几何直观理解:∣∣Ax−b∣∣2就是 Ax 和 b 的欧氏距离,所有可能的 Ax 都在 C(A) 中,而 C(A) 中距离 b 最近的那个点,就是 b 的投影 p,此时 x=x^。
- 代数严格证明:由 ∣∣Ax−b∣∣2=∣∣Ax−p−e∣∣2=∣∣Ax−p∣∣2+∣∣e∣∣2≥∣∣e∣∣2,其中 ∣∣e∣∣2 是与 x 无关的常量,则当 ∣∣Ax−p∣∣2=0 时,取得最小值,此时 Ax=p,即 x=x^
新的方程 Ax^=p,不仅有“一定有解”、“解是最好的”这两个良好的性质,当 Ax=b 本身就有解时,新的方程与原方程的解是一致的,这是因为当 b∈C(A) 时,p=b (上面两种极端情况的第一种)。
也就是说,无论 Ax=b 是否有解,你可以不管三七二十一,就计算 Ax^=p,肯定能解出来一个最好的 x^,它满足“如果有精确解,我就是精确解,如果没有精确解,我就是最好的解”。你可以在对 A 一无所知的情况下,保证能解出一个优秀的 x^。
换一个形式#
为了方便,下面还是假设 A 列满秩。
Ax^=p=A(ATA)−1ATb,我们都知道求逆矩阵既困难又会造成精度问题(浮点数计算时),于是可以两边都左乘 AT,变成
ATAx^ATAx^x^=(ATA)(ATA)−1ATb=ATb=(ATA)−1ATb(1)(2)其中 (1) 是比较好用的形式
而 (2) 在线性回归领域也写作
θ=(XTX)−1XTy并被称为normal equation(或许译作正交方程?)
最小二乘法#
最小二乘法其实可以从投影的角度理解,个人认为这是最巧妙,无需计算的解法了(相比于对均方误差求导的解法)
假设我们有 m 个点 (t1,b1),(t2,b2),…,(tm,bm),要找一条直线 y=cx+d,最佳拟合它们,即令 ∑(cti+d−bi)2(也被称为均方误差,mean square error, MSE)最小。
只需令
b=b1b2⋮bmA=11⋮1t1t2⋮tmx=[dc]就有 Ax=b。假如 m 个点落在同一条直线上,这个方程才有解,大多数情况下,它是无解的,运用前面推导的式子,有
ATA=[m∑ti∑ti∑ti2]ATb=[∑bi∑biti]只需解
[m∑ti∑ti∑ti2][dc]=[∑bi∑biti]即可得到使MSE最小的c和d。
拟合抛物线#
假如将拟合直线变成拟合抛物线 y=c2x2+c1x+c0,只需要改成
b=b1b2⋮bmA=11⋮1t1t2⋮tmt12t22⋮tm2x=c0c1c2然后求 ATAx^=ATb 就完事了,如果把抛物线换成n次多项式也是类似的。
Introduction to Linear Algebra, 5th edition, by Gilbert Strang

